三角形の面積のドリル（座標平面上）

概要

座標平面で、三角形の面積を求める練習します。 「底辺×高さ÷２」ではなく、３点の座標から計算するものです。

簡単な説明

三つの点が（０，０），（ａ，ｂ），（ｃ，ｄ）であらわされているとき、それらをつないだ三角形の面積Ｓは、

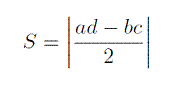
と表されます。つまり、２点のｘ、ｙ座標をたがいちがいに掛け、差をとり、その半分の絶対値です。

絶対値を考えているのは、面積は負にならないからだと思っていいです。 続編として作ろうと思いますが、４角形以上を計算するとき、負の面積を考えると便利なことがあります。

（０、０）が無いとき

三点のうちに（０，０）がない場合は、どれかひとつが（０，０）になるように３点を同じだけ平行移動します。

たとえば、（１，３），（２，８），（−１，４）の場合に、（１，３）を（０，０）に動かすならば、 残りの２点はそれぞれ（２−１，８−３）＝（１，５）と（−１−１，４−３）＝（−２，１）に移るので、 面積Ｓ＝｜１×１−５×（−２）｜／２＝５．５です。

３点を結んで作る三角形の面積を求める問題はよく出されるので、これを知っておくと非常に便利です。

経過

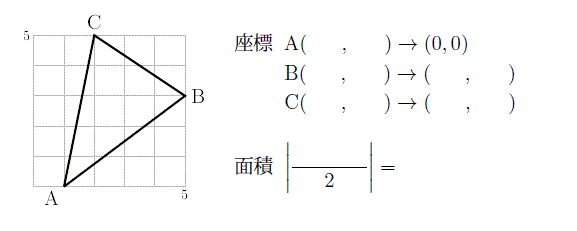
最初につくった座標と三角形の面積１では1点を(0,0)にずらすところまで誘導がついています。説明はつくらなかったので、このページに書いてある通りに計算してください。

PDF

続編

座標入りで作り直していきます。

本文で少しだけ触れていますが、４点以上をつないだ多角形も、これを少し応用するだけでもとまります。 その際の方法は３角形も計算できますし、1個は（０，０）がないといけないということもありません。

ただし、三角形に使うと計算は多くなると思います。私はExcelで土地の面積を計算するときに使いました。日本中の地点に座標が決まってるなんて素敵。